5R parallel leg math model
Introduction
This is basic 5 link log math model needed to calculate position based on input angle.
Prerequirement
Diagram:
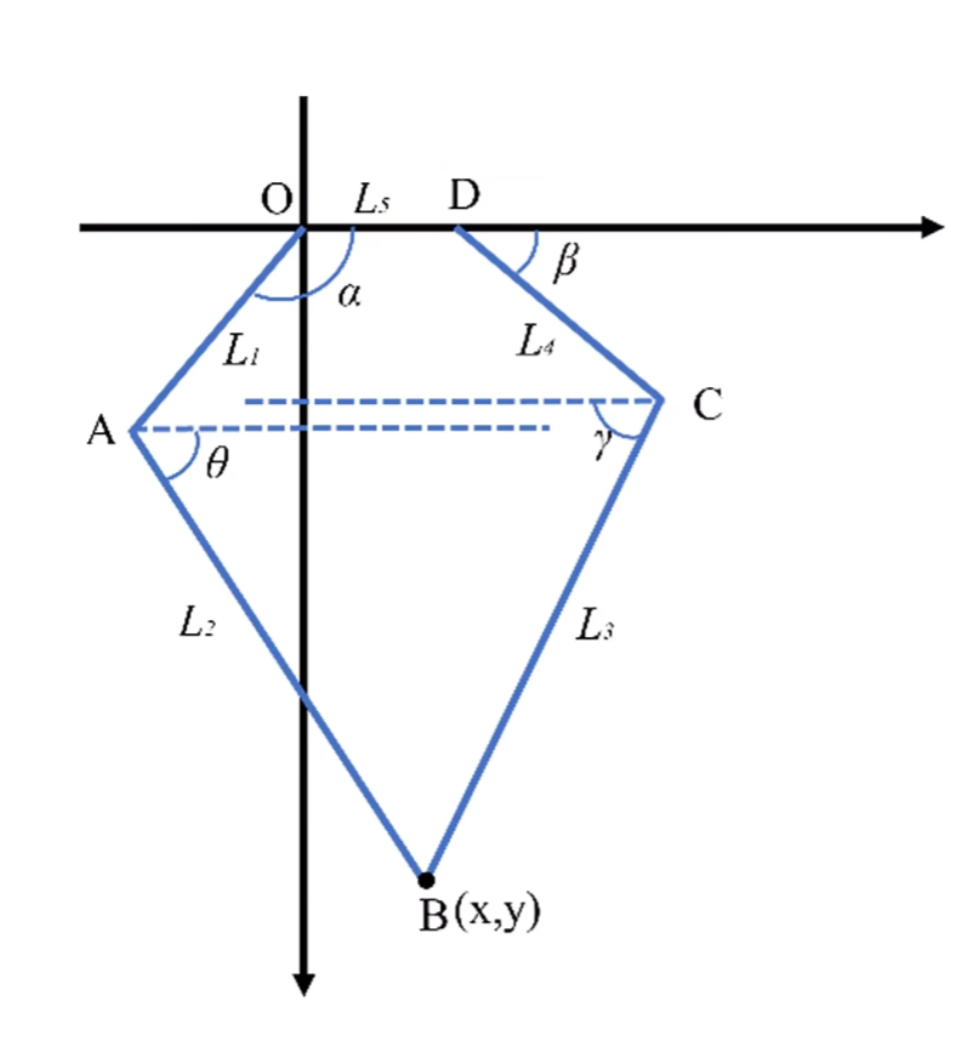
Mathematical Formulation:
Inverse Kinematics Equations
Given:
- Desired position: ( (X, Y) )
- Link lengths: ( L_1, L_2, L_3, L_4, L_5 )
Intermediate variables:
Inverse kinematics solution:
Angle to degrees conversion:
Code
5r-left.cpp
void inverseKinematics(){
// Main inverse kinematics function
void inverseKinematics() {
float alpha1, alpha2, beta1, beta2;
uint16_t servoLeftFront, servoLeftRear;
// Calculate intermediate variables based on geometry and desired position
float aLeft = 2 * IKParam.XLeft * L1;
float bLeft = 2 * IKParam.YLeft * L1;
float cLeft = IKParam.XLeft * IKParam.XLeft + IKParam.YLeft * IKParam.YLeft + L1 * L1 - L2 * L2;
float dLeft = 2 * L4 * (IKParam.XLeft - L5);
float eLeft = 2 * L4 * IKParam.YLeft;
float fLeft = ((IKParam.XLeft - L5) * (IKParam.XLeft - L5) + L4 * L4 + IKParam.YLeft * IKParam.YLeft - L3 * L3);
// Compute possible angles using the inverse kinematics equations
alpha1 = 2 * atan((bLeft + sqrt((aLeft * aLeft) + (bLeft * bLeft) - (cLeft * cLeft))) / (aLeft + cLeft));
alpha2 = 2 * atan((bLeft - sqrt((aLeft * aLeft) + (bLeft * bLeft) - (cLeft * cLeft))) / (aLeft + cLeft));
beta1 = 2 * atan((eLeft + sqrt((dLeft * dLeft) + eLeft * eLeft - (fLeft * fLeft))) / (dLeft + fLeft));
beta2 = 2 * atan((eLeft - sqrt((dLeft * dLeft) + eLeft * eLeft - (fLeft * fLeft))) / (dLeft + fLeft));
// Ensure angles are within 0 to 2π range
alpha1 = (alpha1 >= 0) ? alpha1 : (alpha1 + 2 * PI);
alpha2 = (alpha2 >= 0) ? alpha2 : (alpha2 + 2 * PI);
// Select feasible solution based on expected joint limits
IKParam.alphaLeft = (alpha1 >= PI / 4) ? alpha1 : alpha2;
IKParam.betaLeft = (beta1 >= 0 && beta1 <= PI / 4) ? beta1 : beta2;
// Convert radians to degrees
int alphaLeftToAngle = (int)((IKParam.alphaLeft / (2 * PI)) * 360);
int betaLeftToAngle = (int)((IKParam.betaLeft / (2 * PI)) * 360);
// Adjust angle to match servo neutral at 90 degrees
servoLeftFront = 90 + betaLeftToAngle;
servoLeftRear = 90 + alphaLeftToAngle;
}